关键字: K-means算法
0. 前言
K-means算法是常见的聚类算法。研一的时候在吴桂兴老师的”信息论”课上接触过K-means算法,但并没有深入理解,也没有自己写代码去实现。最近在看斯坦福CS231n课程的lecture2里又涉及到K-means算法,正好也想把Coursera里吴恩达机器学习课程里的代码复习一遍,以此文作为学习总结。
1. 聚类算法概述
在机器学习算法中,按照学习方式来划分,分为有监督学习、无监督学习、半监督学习、强化学习。其中,在无监督学习(supervised learning)中,训练的样本的标记信息是未知的,我们的目标是对无标记训练样本的学习来揭示输入数据的内在性质和规律,从而可对数据进行下一步的分析。“聚类算法”是无监督学习中经常使用的算法。
那么聚类是如何实现的了?通常来说,聚类是将数据集中的样本划分为若干个不相交的子集,每个子集称为一个簇(cluster),并且每个子集可能都对应于一些潜在的类别。举个例子,某招聘会上有一群毕业生,有的是”交大毕业生”,有的是”科大毕业生”,有的是”上大毕业生”,这三个子集互不相交,且都是这群毕业生的组成部分。但我们需要注意的是,这些类别,或者说聚类产生的子集的概念,对于聚类算法而言事先是未知的。聚类过程仅能自动形成簇结构,簇所对应的概念语义需要人为的把握和命名。
聚类算法既能够作为一个单独的过程,用于寻找数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。举个例子,在一些商业应用中,我们需要对新用户的用户类型进行判别,然而”用户类型”的概念很难全面准确地被商家定义,于是我们可以针对已有的用户数据进行聚类,将聚类结果的每一个簇定义为一个类,然后再根据这些类来训练分类模型,达到判别新用户的类型的目标。
2. k-means算法
2.1 k-means算法概述
k-means算法,也称为k均值聚类算法,是最广泛使用的聚类算法。它实现的是,将数据集中的n个点划分到k个聚类中,使得每个点都属于离此点最近均值点所对应的聚类。k-means算法优点在于简单、快速,但其缺点也很明显。使用k-means算法就必须要求事前给出k值,也就是预先确定好想要把数据集分成几类。其次,不同的初始化点,最后通过k-means得出的聚类结果也有可能产生差异。最后一点,k-means对于”噪声点”是极其敏感的,可能极少的”噪声点”都会对最后的结果产生很大的影响。
2.2 k-means算法流程

算法流程说明:第1行对均值向量进行初始化,再第4-8行与第9-16行依次对当前簇划分及均值向量迭代更新,若迭代更新后聚类结果保持不变,则在第18行将当前簇划分结果返回。
3. matlab代码实现
在Coursera的吴恩达的机器学习的课程作业里,ex7中有关于k-means的matlab实现。我将其代码进行合并和改进,源码如下:
1 | function kmeans() |
在matlab命令行中敲入run kmeans()命令,即可执行脚本程序。
实验的效果图如下:
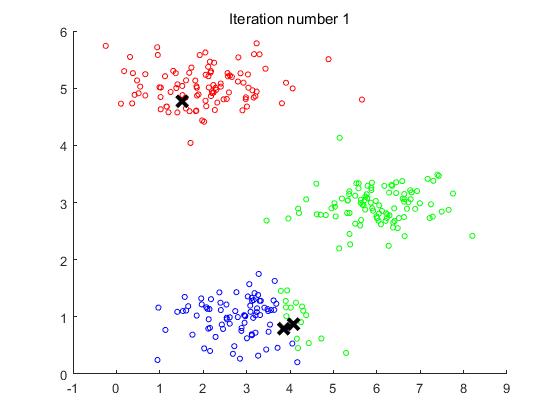
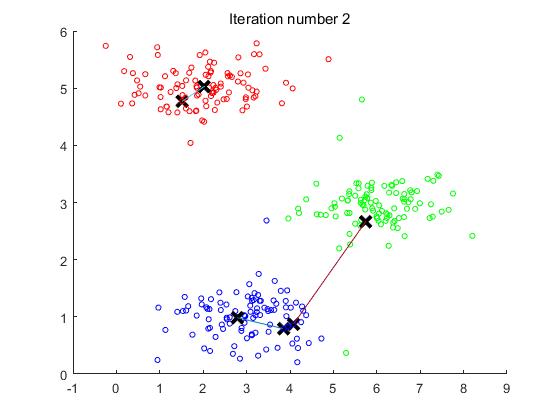
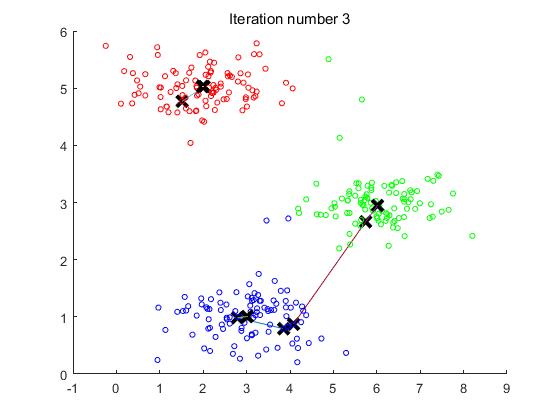
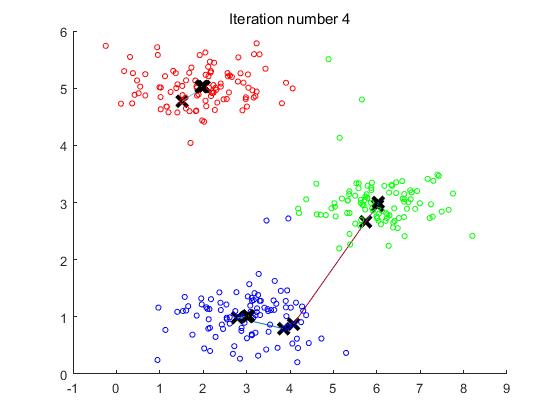
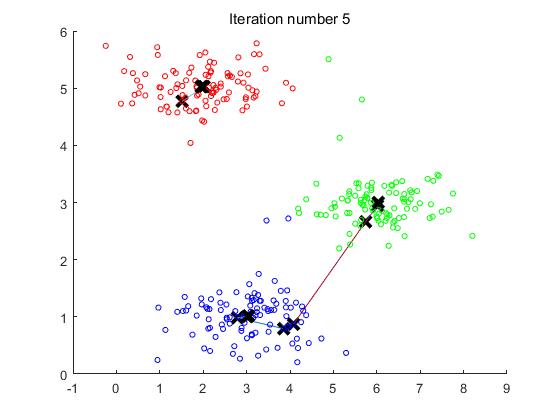
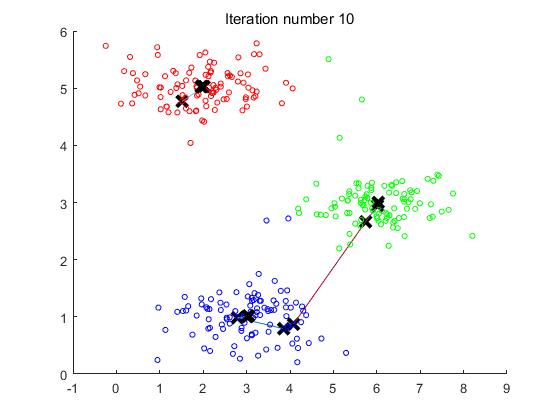
观察图可以看出,中心点在迭代第四次之后便不再更新,所以第四次迭代之后的图便不再发生变化。
对应的代码和数据集的下载链接:https://pan.baidu.com/s/14yIoSxEiIeir2VaRR2qJlQ 密码:ts8l。
参考文献: